Engineering mechanics Math

Example:

Two rough planes inclined at 30° and 60° to horizontal are placed back to back as shown in Fig.. Two blocks weighing 60 N and 120 N respectively are placed on the faces inclined at 30° and 60' respectively and are connected by a string running parallel to planes and passing over a frictionless pulley. If the coefficient of friction between planes and blocks is 0.3, find the resulting acceleration and tension in the string?

Solution: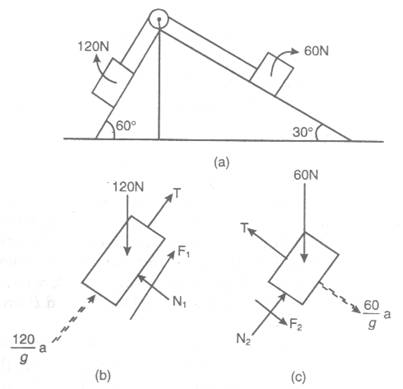

Let the assembly move down the 60° plane by an acceleration 'a' m/sec². Free body diagrams of 120 N and 60 N blocks along with inertia forces are shown in Figs. (b) and (c) respectively.

Consider the block weighing 120 N:

S Forces normal to the plane = 0 gives

N₁ = 120 cos 60° = 60 N                                                                 (i)

From the law of friction

 

F₁ = mN₁, = 0.3 × 60 = 18 N

 

S Forces parallel to the plane = 0 gives                                                   (ii)

T + 120 / 9.81 a + F₁ – 120sin60° = 0 9.81

T + 120/ 9.81 = 120 sin 60°– F₁

 

= 120 sin 60°–18

 

= 85.923                                                                     (iii)

 

Now consider 60 N block:

 

S Forces normal to plane = 0 gives

 

N₂ = 60 cos 30° = 51.926N                                                            (iv)

 

From the law of friction,

 

F₂ = mN₂ = 0.3 × 51.926 = 15.588 N                                             (v)

 

S Forces parallel to 30° plane = 0

 

60 sin 30° + F₂ + 60 / 9.81 a – T = 0

 

60 / 9.81 a – T = –60 sin 30° – 15.588,                             since F₂ = 15.588 N

 

\ 60 / 9.81 a – T = –45.588

 

Adding eqns. (iii) and (vi), we get

 

180 / 9.81 a = 85.923 – 45.588 = 40.335

 

a = 2.19825 m/sec²

 

Substituting the value of acceleration 'a' in eqn. (iii), we get

 

7 + 120 / 9.81 × 2.19825 = 85.923 9.81

 

T = 59.033 N